PALMER: Perception-Action Loop with Memory for Long-Horizon Planning

This is enabled by a two-step process. First, we learn a latent space where the distance \(d_\phi = \|z_1 - z_2\|\) between the representations of two states \((s_1, s_2)\) captures how many timesteps it takes for an optimal policy to go from \(s_1\) to \(s_2\) (i.e., reachability between states). To achieve this, we use the goal-conditioned value function \(Q(s_1,a,s_2)\) estimated through offline hindsight relabelling for contrastive representation learning. We employ a loss function that dictates that whenever two states are close according to Q-values, \(d_\phi\) should be small.

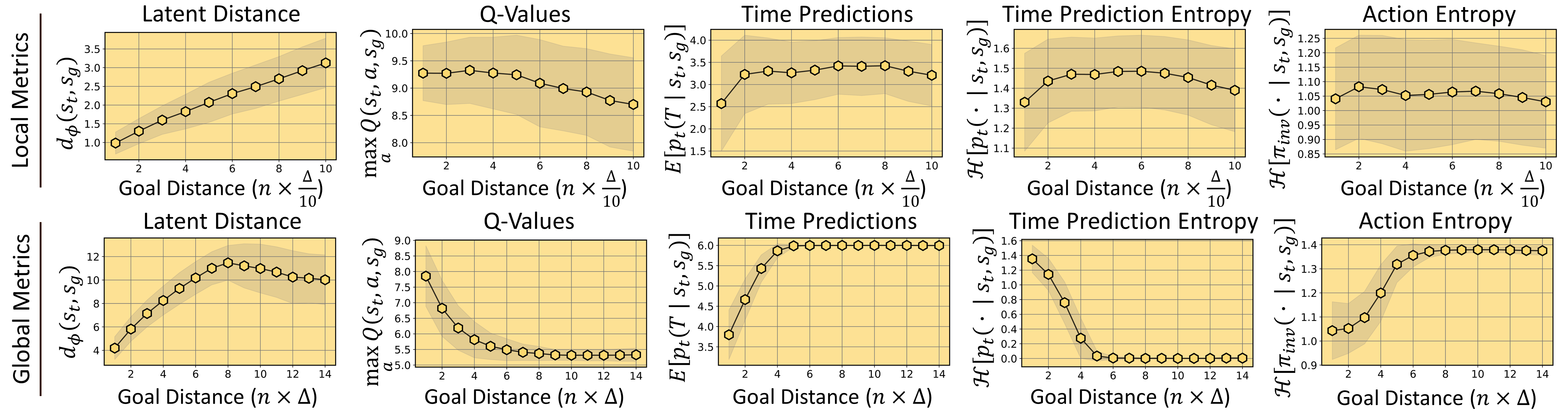
Comparison of latent distances \(d_\phi\) with other suitable metrics. While all metrics are reasonably monotonic with reachability (i.e., goal distance), only \(d_\phi\) does not saturate when evaluated locally (i.e., for close by goals). In addition, the ratio between the variance of \(d_\phi\) and the slope of its mean is much smaller compared to other sensible metrics (i.e., \(d_\phi\) has a high signal-to-noise ratio).

Second, we threshold this learned latent distance metric \(d_\phi\) to define a neighborhood \(\mathcal{N}_{r}(s)\) around a given state \(s\), where \(\mathcal{N}_{r}(s) = \{s_n \ | \ d_\phi(s, s_n) \leq r\}\). Given a starting state \(s_c\) and a goal state \(s_g\), we then search the replay buffer \(\mathcal{M}\) for the trajectory segment \(\tau\) that achieves the highest reward \(\mathcal{R}(\tau)\) while starting from a state \(\tau_{0}\) in \(\mathcal{N}_{r}(s_c)\) and ending in a state \(\tau_{-1}\) in \(\mathcal{N}_{r}(s_g)\). This corresponds to the following optimization problem: \[ \tau_{\mathcal{M}(s_c, s_g)} := \arg\max_{\tau \in \mathcal{M}} \: \: {\mathcal{R}(\tau)} \quad \textrm{s.t.} \quad \tau_{0} \in \mathcal{N}_{r}(s_c) \ , \ \tau_{-1} \in \mathcal{N}_{r}(s_g) \] We call this trajectory retrieval process 'Perceptual Experience Retrieval' (PER). We use it only to retrieve short trajectory segments between close-by states \((s_c, s_g)\). These short segments are then stitched together into long global trajectories using the planning algorithms defined in the next section.

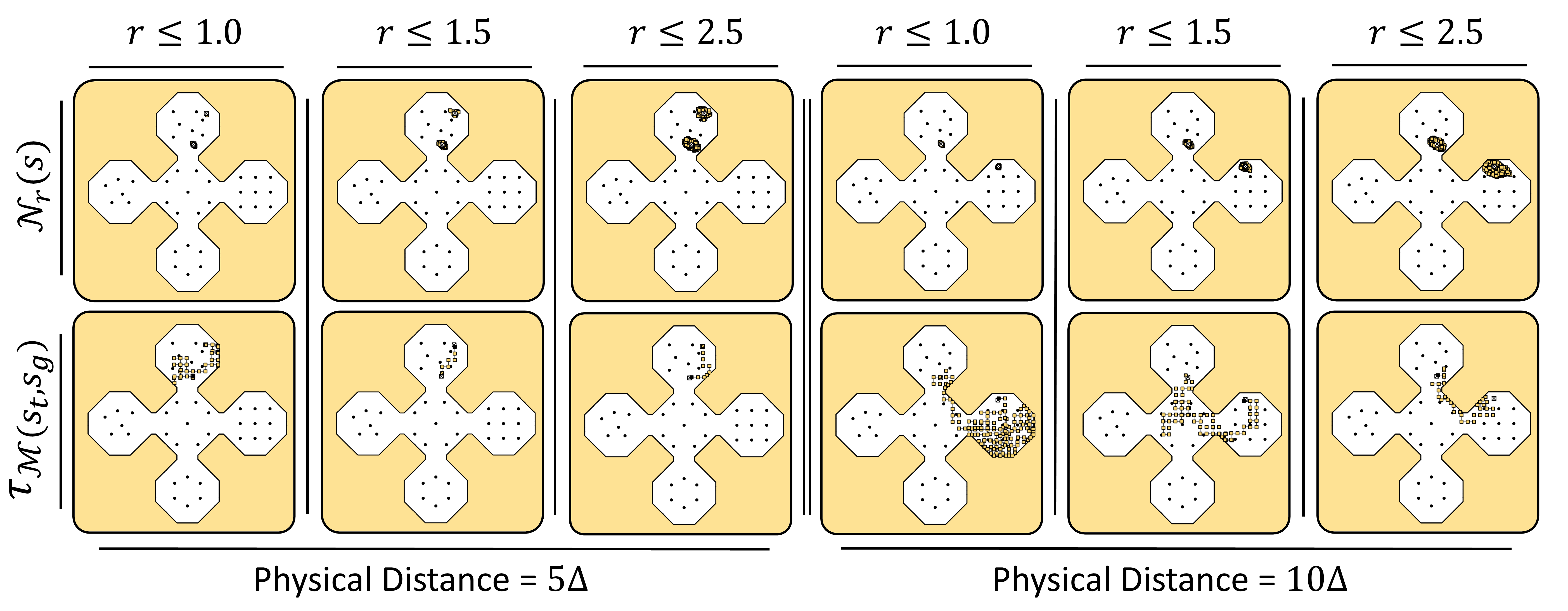
Visualizations of neighborhoods \(\mathcal{N}_{r}(s)\) and corresponding trajectory segments \(\tau_{\mathcal{M}(s_t, s_g)}\) retrieved using PER. As the neighborhood radius \(r\) increases, nearest neigbors extend further away from the query state. As a result, the retrieved trajectory gets shorter since the number of trajectory segments \(\tau \in \mathcal{M}\) whose endpoints satisfy the neighborhood constraints increases.

Classical sampling-based planning algorithms such as RRT or PRM connect points sampled from obstacle-free space with line segments in order to build a planning graph. We instead reimagine them as memory search mechanisms by altering their subroutines so that, whenever an edge is created, a trajectory is retrieved from the replay buffer through PER and stored in that edge. Our new definitions for these subroutines directly mirror the original ones given in [ref]:

1. Sampling: Sampling originally returns a point from obstacle free space. We instead return a state \(s_c\) from the replay buffer \(\mathcal{M}\) using any distribution (e.g., uniform, or based on visitation-counts).
2. Lines and Their Cost: The equivalent of drawing a line segment in our framework is retrieving a trajectory \(\tau_{\mathcal{M}(s_c, s_g)}\), and its length and cost are \(len(\tau_{\mathcal{M}(s_c, s_g)})\) and \(-\mathcal{R}(\tau_{\mathcal{M}(s_c, s_g)})\) respectively.
3. Nearest State and Neighborhood Queries: Given a query point \(s_i\), these subroutines return the closest point or a neighborhood of points within a distance, among a set of vertices \(V = \{s_j\}\). We preserve these definitions, and only replace the metric from euclidean distance to \(len(\tau_{\mathcal{M}(s_c, s_g)})\).
$$\begin{eqnarray} Nearest(V, s_g) &:=& \arg\min_{s_c \in V}{ \, len(\tau_{\mathcal{M}(s_c, s_g)})} \nonumber \\ Near(V, s_g, r) &:=& \{s_c \in V \ | \ len(\tau_{\mathcal{M}(s_c, s_g)}) \leq r\} \nonumber \\ \end{eqnarray}$$
4. Collision Tests: Collision tests originally prevent the sampling and line drawing subroutines from intersecting obstacles. Since we are planning in retrospect, any such undesirable event can be handled during PER by adjusting the reward function (i.e., if \(\tau\) has such an event, this reflects on \(\mathcal{R}(\tau)\)).

Using these subroutines directly in-place of their originals, we reimplement retrospective equivalents of PRM, RRT, and RRT*, which we call R-PRM, R-RRT, R-RRT*. Like their classical counterparts, our proposed planning algorithms can also be used to optimize any general reward function \(\mathcal{R}\). As the number of sampled vertices increases, \(\mathcal{R}(\tau_{\mathcal{M}^{\text{*}}(s_c, s_g)})\) gets optimized through dynamic programming (i.e., by minimizing the Bellman error between vertices of the planning graph).

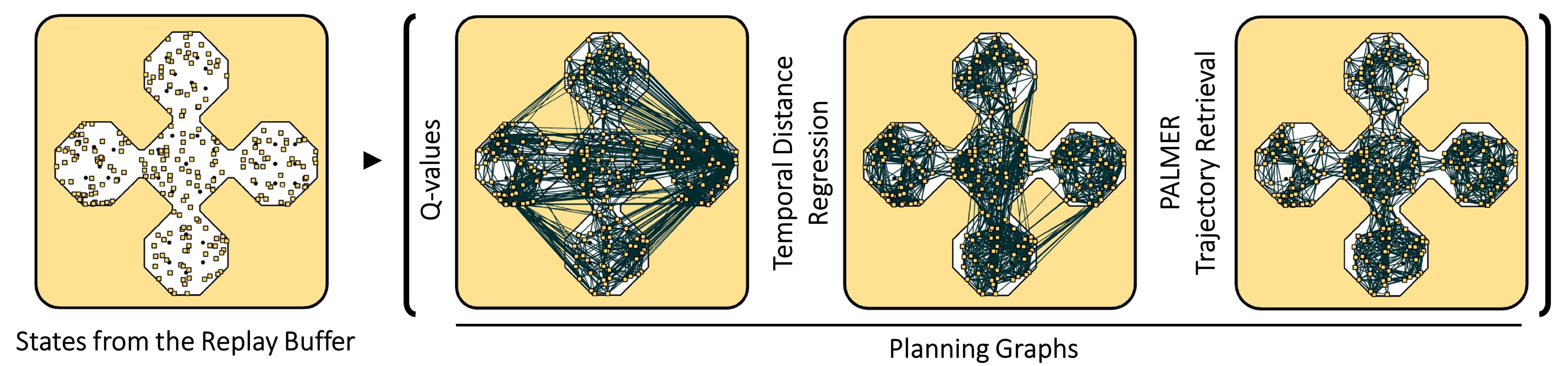
We repurpose classical sampling-based planning algorithms as memory search mechanisms, by altering their subroutines so that whenever an edge is created a trajectory segment is retrieved through PER and stored in that edge. Computing shortest paths over the resulting planning graphs restitch these trajectory segments into a long trajectory. The visualizations above show planning graphs produced by R-PRM, R-RRT, R-RRT*, and resulting restitched trajectories.

Given only an offline replay-buffer of 150k environment steps collected from a uniform random-walk, PALMER can allow image-based navigation between any two points in reconstructions of large-scale real-world apartments from the Habitat simulator. The limited amount of data (i.e., compared to sample complexities around the orders of magnitude 1e6-1e7 common in RL) and the offline RL setup make this an exceptionally challenging setting, as indicated by the performance of the baselines.

To test our method on a continuous control task, we also perform experiments on the Maze2D benchmark. As shown in the table, we find that PALMER achieves strong performance, and can solve mazes of all three complexities.

Planning graphs created by PALMER are significantly more robust to hallucinated shortcuts compared to baselines. This is because creating an edge between two states requires there to be an actual trajectory segment in the replay-buffer that connects them. By definition, states that are far apart from each other in-terms of reachability are rarely observed together in an experiential learning framework (e.g., within the same RL episode, or within close by time-steps during random exploration). As such, for any model that uses hindsight relabelling to estimate the proximity between current-goal state pairs (e.g., through Q-learning or direct regression), if it is trained solely on the observed distribution of experiential data, far apart state pairs will be out of distribution (i.e., they have a low probability of being sampled under the experiential data distribution). This means estimates for such pairs will inevitably be inaccurate. This highlights the importance of memory as a robustification mechanism: in order to determine whether two states are close or not, PALMER explicitly tries to remember if they were ever actually observed within the same segment of past experience.